Markus Pister - private Homepage

Besuchernr.:

Kontakt:
mp0032@mapisano.de

Inhaltsverzeichnis

• Home
• Checklisten
• Immobilienkauf
• Finanzthemen
• Publikationen
  • Morphologie
• Sonstiges

Morphologie (Hauptseminarbeitrag)

Inhaltsverzeichniss

1. Der Begriff Morphologie
2. Morphologische Grundoperationen
   1. Minkowski-Addition
   2. Minkowski-Subtraktion
   3. Dilatation und Erosion
   4. Hit-or-Miss Transformation
   5. Anwendungen
3. Morphologische Filter 
   1. Opening
   2. Closing
   3. Anwendungen
4. Morphologische Operatoren und Sequentielle Operationen 
   1. Thinning
   2. Sequentielles Thinning
   3. Pruning

1. Der Begriff Morphologie

Fast jeder von uns kennt Werbungen, in denen ein Menschenkopf zu einem Tierkopf wird oder sich Objekte verwandeln. Auf die Frage hin, was das für ein Vorgang sei bekommt man meistens die Antwort: Das ist Morphing !

Tatsächlich ist im allgemeinen Sprachgebrauch Morphologie die Lehre vom Bau oder von Oberflächen von Dingen und von deren Veränderungen mit der Zeit. So ist zum Beispiel in der Biologie das Erwachsenwerden hinsichtlich des Körperbaus ein morphologischer Vorgang. Genauso ist in der Geologie die Veränderung der Oberflächenformen ein morphologischer Vorgang.

In der Mathematik ist Morphologie die Erforschung der Topologie oder Struktur von Objekten mittels ihrer Darstellung. [Jai89] Es wird also ein Bild als eine Punktmenge im Raum betrachtet. Die Gestalt des Bildes soll mittels Operationen mit einer anderen strukturierenden Menge in eine aussagekräftigere Form gebracht werden.

In der Bildverarbeitung versucht man Bilder in Übereinstimmung mit der Beurteilung durch das menschliche Auge in aussagekräftige Einheiten und Texturen zu zerlegen. Man benutzt genauso wie in der Mathematik ein strukturierendes Element mit dem man die Formen verändert.

2. Morphologische Grundoperationen

Im weiteren werden nun ein paar morphologische Grundoperationen erklärt und vorgeführt.

Um die Erklärung und Darstellung zu vereinfachen, beziehen sich die Beispiele auf einfarbige Bildmengen (Regionen) in Ebenen. Analog gibt es diese Operationen auch bei mehrfarbigen Mengen im Raum.

2.1. Minkowski-Addition

Bei der Minkowski-Addition wird eine Bildmenge X mit einem strukturierendem Element S vergrössert. Mathematisch beschrieben ist die Ergebnismenge die Menge aller Punkte, die als Vektorsumme eines Punktes aus X und eines Punktes aus S gebildet werden können.

X ⊕ S = {y | y=x+s,x ∈ X,s ∈ S}

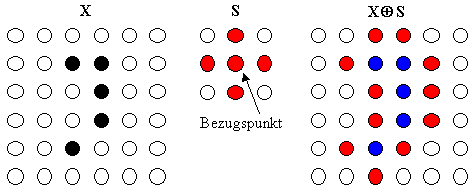
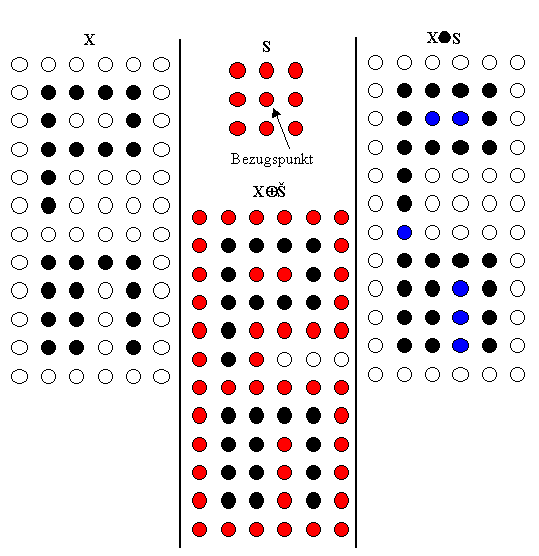
Zum besseren Verständniss nochmal eine weniger mathematische Beschreibung: Man legt den Bezugspunkt des strukturierenden Elements S auf jeden Punkt des Bildes X und zeichnet jedesmal das Element S an diese Stelle.

Bildlich kann man sich diese Addition meistens so vorstellen, daß man mit dem Bezugspunkt des strukturierenden Elements einmal um den Rand des Bildes X herumfährt und dort alle Punkte markiert, die von dem strukturierenden Element S überdekt werden.

Die Minkowski-Addition wirkt somit vergrössernd, falls ein das strukturierende Element mehr als einen Punkt hat. Somit dient die Minkowski_Addition zum: -Vergrösern von Regionen -Verkleinern von Löchern -Löschen von kleinen Löchern -Schließen von Lücken in und zwischen Regionen

2.2 Minkowski - Subtraktion

Bei der Minkowski-Subtraktion wird eine Bildmenge X mit einem strukturierenden Element S verkleinert. Mathematisch beschrieben ist die Ergebnismenge die Menge aller Punkte, die nach der Differenzbildung mit einem Punktvektor aus S noch in der Bildmenge X liegen.

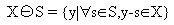
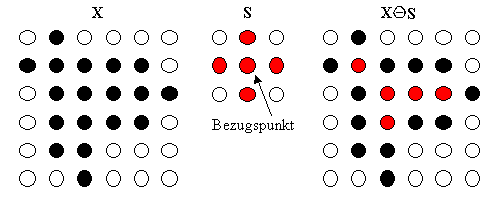
Wiederum wie bei der Minkowski-Addition eine weniger mathematische Beschreibung zum besseren Verständnis: Man entferne von der Bildmenge X alle die Punkte, die zu einer Schnittmenge mit S gehören, wenn der Bezugspunkt von S irgendwo außerhalb von X liegt.

Bildlich kann man sich diesen Vorgang folgendermaßen vorstellen:
Man fährt mit dem Bezugspunkt des strukturierenden Elements einmal um den Rand des Bildes X herum und löscht dabei alle Punkte, die dabei mit dem strukturierenden Element überdeckt werden.

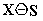
Die Minkowski-Subtraktion wirkt verkleinernd, wenn das strukturierende Element größer als ein Pixel ist. Sie dient also zum:
-Verkleinern von Regionen
-Vergrößern von Löchern
-Löschen von kleinen Regionen
-Abbrechen von Brücken zwischen Regionen

2.3. Dilatation und Erosion

Mathematisch gesehen sind die Begriffe Dilatation und Erosion schnell erklärt:

Dilatation ist im Prinzip das gleiche wie eine Minkowski-Addition, nur wird das strukturierende Element S zuvor an seinem Bezugspunkt punktgespiegelt.
Analog ist Erosion im Prinzip das gleiche wie Minkowski-Subtraktion, nur wird auch hier das strukturierende Element S zuvor gespiegelt.

X ⊕ Š = {y | y=x-s,x ∈ X,s ∈ S}

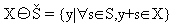
Bei einem punktsymmetrischen strukturierendem Element ist es egal, ob man Dilatation und Erosion oder Minkowski-Addition und -Subtraktion benutzt. Bei strukturierenden Elementen, die nicht Punktsymmetrisch sind, sind die Unterschiede jedoch deutlich spürbar.

In eine weniger mathematischen Weise beschrieben ist die Dilatation folgendermaßen zu verstehen:
Man zeichnet den Bezugspunkt des strukturierenden Elements S auf, wenn dieses eine Überschneidung mit der Bildmenge X hat.

An folgendem Bild sollte der Unterschied zur Minkowski-Addition deutlich werden:

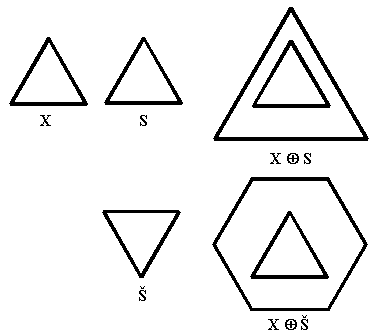
Die Erosion kann man folgendermaßen Beschreiben:
Man setze den Bezugspunkt des strukturierenden Elements S immer dann, wenn das strukturierende Element komplett in das Bild X hineinpaßt.

Auch hier eine Graphik, die den Unterschied zur Minkowski-Subtraktion deutlich machen soll:

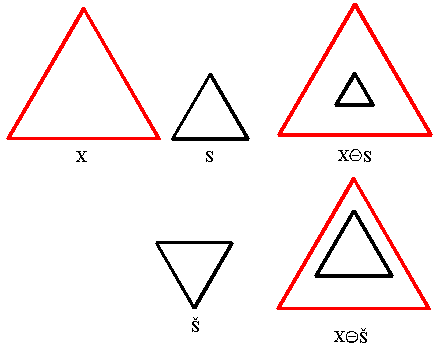
2.4. Hit-or-Miss-Transformation

Die Hit-or-Miss-Transformation ist eine Erweiterung der Erosion. Im Vergleich zur Erosion benutzt man jedoch zwei strukturierende Elemente S' und S''. Das erste Element S' wird genau wie bei der Erosion verwendet. Es muß jedoch zusätzlich an der gleichen Stelle das Element S'' so passen, daß die Punkte des Bildes X keine Überschneidung mit den Punkten des Elements S'' haben. Es wird also sowohl auf vorhandene, wie auch auf nicht vorhandene Umgebungspunkte geachtet. Mathematisch ist die Hit-or-Miss-Transformation folgendermaßen definiert:

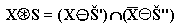
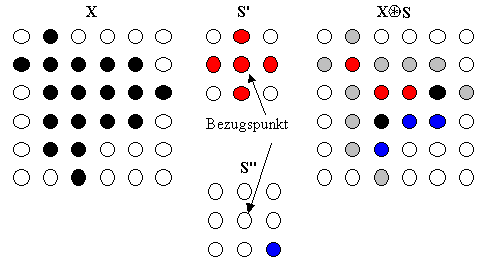
So verbleiben bei der Hit-or-Miss-Transformation in diesem Beispiel nur die zwei schwarzen Punkte, die beide Bedingungen erfüllen.

Diese Transformation eignet sich besonders zum finden von Ecken oder Randpunkten von Objekten.

2.5. Anwendungen

Zusammenhang:
Eine sehr einfache Anwendung der Dilatation ist es, nah beieinanderliegende Objekte zu erkennen. Dazu werden einfach die Objekte vergrößert, bis sie sich überschneiden. Alle Objekte, die dabei verschmolzen sind gehören zueinander. In dem folgenden Beispiel sieht man die zusammengehörenden hellen Bereiche.

 

Als strukturierendes Element verwendet man zum Beispiel eines wie in der obigen Zeichnung zum entfernen von einzelnen Punkten. Der freibleibende Bezugspunkt bei Einzelpunkten läßt diese bei einer Schnittmengenbildung von der Bildmenge X und der Dilatierten Menge verschwinden.

 

Suchen von Eigenschaften:
Mit Hilfe der Erosion lassen sich bestimmte Eigenschaften von Objekten erkennen. So kann man zum Beispiel mit einer waagrechten Linie als strukturierendem Element aus einer Menge von Büroklammern die waagrecht liegenden von ihnen erkennen.

Die Rekonstruktion der erkannten Klammern erfolgt durch eine wiederholte Dilatation der Treffermenge mit einer darauffolgenden Schnittmengenbildung mit der Bildmenge X.

Buchstabenerkennung:
Mit der Hit-or-Miss-Transformation lassen sich Buchstaben bis zu einem gewissen Grad erkennen, indem man die strukturierenden Elemente als Schablone verwendet.

 

In diesem Beispiel soll der Buchstabe P erkannt werden. Eine reine Erosion (rot) erkennt auch das B und das R, da in ihnen ein P enthalten ist. Die Hit-or-Miss-Transformation (weiß) erkennt nur das P. Das untere P wird jedoch nicht erkannt, da die P-Schablone nicht hineinpaßt. Vergrößert man nun mit einer Dilatation die Buchstaben, so kann man das untere P erkennen.

3. Morphologische Filter

Morphologische Filter sind laut Definition eine sequentielle Anwendung von morphologischen Grundoperationen. Dabei soll allerdings die sequentielle Anwendung eines Filters keine weiteren Änderungen hervorrufen. Im folgenden werden nun zwei Filter beschrieben, die auf Basis von Dilatation und Erosion arbeiten.

3.1 Das Opening

Das Opening ist definiert als eine Erosion mit einer anschließenden Minkowski-Addition.

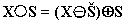
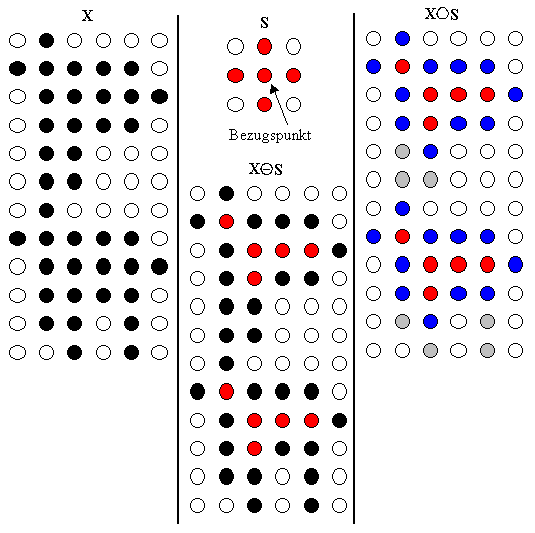
Die Grauen Punkte werden in diesem Bild also herausgefiltert. Der Opening-Filter entfernt durch seine Erosion kleine Objekte,Brücken und Spitzen von Objekten, erhält aber durch die darauf folgende Minkowski-Addition die Größe des Objektrumpfes.

Bei diesem Bild kann man gut erkennen, wie die rechte Brücke abgebrochen wird und einige Spitzen entfern werden.Der Rest des Rumpfes bleibt erhalten.

3.2. Das Closing

Als Gegenstück zum Opening ist das Closing definiert als eine Dilatation mit einer anschließenden Minkowski-Subtraktion.

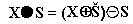
Das Closing wirkt durch die Dilatation vergrößernd und dient somit zum Auffüllen von Spalten, Verbinden von Objekten und zum Auffüllen von Löchern. Durch die anschließende Minkowski-Subtraktion versucht man die Größe des Objektrumpfes zu erhalten.

Bei diesem Bild wird mit einem Quadrat als strukturierendem Element das Bild geschlossen. Deutlich erkennt man dabei das Auffüllen des Loches und der Spalten. Die linke Brücke wird dabei auch erstellt.
 

3.3 Filter-Anwendungen

Um die Anwendung morphologischer Filter zu demonstrieren soll folgendes Beispiel dienen:

 

Die Maschine aus dem linken Bild soll aus dem Bild herausgeschnitten werden. Dazu wird mit dem Segmentationsverfahren Region_Growing zuerst die Maschine grob herausgeschnitten. (rot und blau).
Dabei wird aber zu viel herausgeschnitten, wie zum Beispiel der Kabelrand links oben. Mittels Opening werden diese Spitzen entfernt (blau). Es werden aber auch besonders im oberen Bereich der Maschine winzige Löcher vergrößert.

 

Nun sollen die Löcher des geöffneten Bildes gefüllt werden. Dazu verwendet man den Closing-Filter.(grün) Wie man sieht, werden Spalten und Löcher geschlossen, ohne die Figur der Maschine zu ändern.
Als leztes sollen nun mit einem noch gröberen Opening-Filter die verbleibenden Spitzen am oberen Ende der Maschine entfernt werden. Das Ergebnis ist im Bild rechts zu sehen.(gelb)

4. Morphologische Operatoren und Sequentielle Operationen

Die nächste Erweiterung zu den Filtern sind Morphologische Operatoren. Auch sie entstehen aus der sequentiellen Anwendung von den Grundoperationen, es darf jedoch im Gegensatz zum Filter eine nochmalige Anwendung des Operators eine weiter Veränderung hervorrufen.

So kann man auch mit der sequentiellen Anwendung dieser Operatoren eine Veränderung deer Bildmenge verursachen.

Im folgenden wird eine kleine Auswahl aus diesem Bereich vorgestellt.

4.1 Thinning

Beim Thinning wird eine Hit-or-Miss-Transformation mit einem strukturierendem Element S auf einer Bildmenge X ausgeführt. Die daraus folgende Ergebnissmenge wird dann von dem ursprünglichen Bild X subtrahiert.

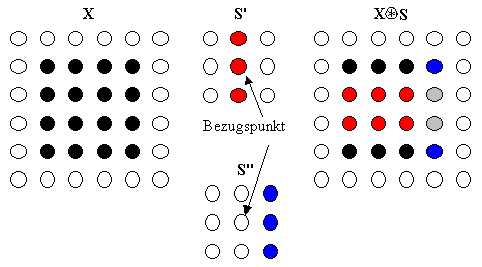
Bei diesem Beispiel wurden die beiden Hellgrauen Punkte entfernt. In diesem speziellen Beispiel verändert ist ein weiterer Aufruf von Thinning nichts mehr. Allgemein ist dies jedoch nicht der Fall.

4.2 Sequentielles Thinning

Das seuentielle Thinning ist im allgemeinen Sprachgebrauch auch als Skelletieren bekannt. Dabei wird mit den folgenden strukturierenden Elementen ein je ein Thinning gemacht.

Die blauen Punkte des Elements entsprechen denen, die in der Bildmenge X enthalten sein sollen, die roten Punkte denen, die in der Bildmenge X nicht enthalten sein sollen.

Nachdem man diese 8 Thinning-Operationen einmal ausgeführt hat, ist der Rand der Bildmenge von allen Seiten abgetragen worden, falls die Breite der Bildmenge X nicht nur noch 1 Pixel gewesen ist.

Bei mehrfachem Anwenden dieser Operationen kann eine Bildmenge so lange reduziert werden, bis nur noch Linien der breite 1 Pixel übrig bleiben.

4.3. Pruning

Wie man bei der Sequentiellen Anwendung des Thinnings erkennen konnte bleiben öfters Zweige zurück, die unerwünscht sind. Zum Entfernen von Zweigen bis zu einer bestimmten Länge gibt es die Pruning-Operation.

Die Vorgehensweise der Pruning-Operation soll an folgendem Beispiel zum Entfernen von Zweigen bis zu einer Länge von 2 Punkten beschrieben werden:

Zuerst verkürze man alle Zweige um die Länge 2 durch Anwenden des Thinning-Operators mit dem strukturierenden Element S. Dabei wird S jeweils um 90° gedreht und dann zweimal benutzt. Das Ergebnis kann man in der Menge X1 sehen: Es sind alle Zweige um zwei Punkt verkürzt worden.
Danach wird mit S eine Hit-or-Miss-Transformation ausgeführt, wobei S wieder jeweils um 90° gedreht wird und die Vereinigungsmenge X2 der Ergebnismengen weiterverwendet wird. Damit erkennt man die Zweigenden der Zweige, die länger als zwei Punkt gewesen sind.
Die Menge X2 wird dann mit dem strukturierenden Element D zweimal dilatiert und die Ergebnismenge mit dem Bild X geschnitten. Dadurch erhält man die Zweigenden, die nicht Abgeschnitten werden sollen.
Vereint man nun die Bildmenge X1, bei der alle Zweige um zwei Punkte gekürzt geworden sind, mit der Menge der Zweigenden, die erhalten bleiben sollen, so bekommt man als Ergebnismenge die Menge XP, bei der alle Zweige, die kleiner oder gleich zwei Punkte sind, entfernt worden sind.

In diesem Beispiel sind die roten Zweige entfernt worden.